ARK is responsible for development of the satellite prediction library libpredict, on which we earlier have published a couple of blog posts (see e.g. https://www.la1k.no/tag/libpredict/, https://www.la1k.no/tag/flyby). This library is based on the satellite prediction program Predict, which we have forked into the user application Flyby, while the satellite prediction functionality was forked into libpredict. Flyby uses libpredict to calculate satellite orbits, instead of having both UI and satellite prediction code in the same application, allowing reuse of satellite prediction code in other applications and to separate the development of the two.
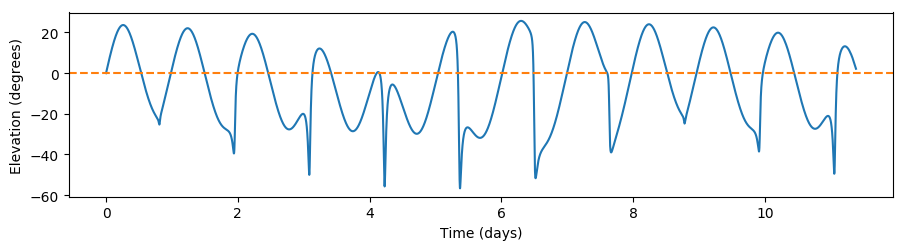
Among libpredict’s features are functions for estimating the AOS and LOS of a satellite. AOS (arrival of satellite, or acquisition of signal) and LOS (loss of satellite, loss of signal) are defined respectively as the time when the satellite arrives over the horizon, and when the satellite passes below the horizon. Plotting the elevation as a function of time, AOS and LOS show up as the intersections between the elevation curve and the horizon line:
Estimating AOS and LOS is then a matter of finding the roots of this curve down to some precision, hopefully without using too many iterations and without skipping any passes. There are many well-defined mathematical techniques for finding such roots numerically. There is much information available when predicting satellite orbits, and it is not strictly a black box that can only be evaluated based on the elevation curve. Clever finding of AOS and LOS should also exploit the other available information to reduce the number of necessary iterations.
libpredict has inherited its algorithms for finding AOS and LOS from predict. We haven’t done much about these, since they do the job well enough, although in a bit mystical way and not necessarily very mathematically correct. It bases itself on some mysterious step functions like
time_step = 0.00035*(elevation*((altitude/8400.0)+0.46)-2.0).
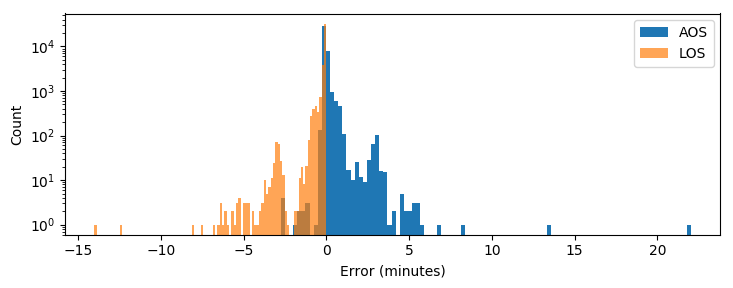
Where do they come from? No idea! The interesting thing is to evaluate how well they estimate the AOS and LOS. Not that bad, as it turns out. We’ve downloaded all TLEs available on celestrak.com, stepped through a couple of passes for each TLE at 1 minute precision, and estimated a “correct” AOS/LOS by finding the roots of a natural cubic spline fit of the elevation curve. These “correct” AOS/LOS estimates were compared against AOS/LOS as estimated using libpredict, and a histogram over the errors was generated.
Most of the errors are well below 1 minute, but some also between 0 and 5 minutes. The larger errors are for satellites far out in space, which have passes that can last over multiple days due to both the slowness of the orbit and the rotation of Earth:
An error of 5 minutes is not that large compared to the duration of the pass.
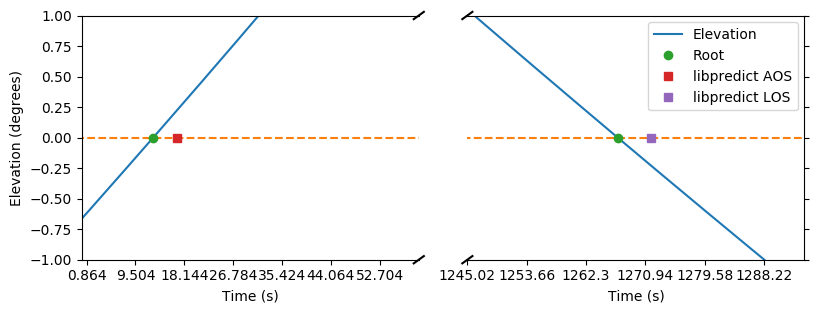
The error in LOS in the error histogram above is always negative, which means that libpredict’s LOS is calculated to always be after our interpolated LOS. Illustration of this in an elevation curve:
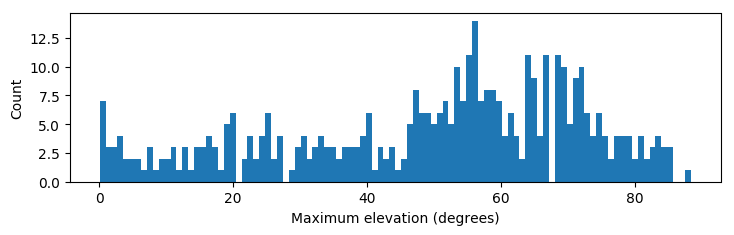
We ran over 6331 TLEs, with a number of passes of order between 10 000 and 100 000. Out of these passes, we missed a number of 417 completely using libpredict’s approach. At first, I was thinking that this was due to these passes being outside libpredict’s threshold for what constitutes as a pass, but turns out that passes with maximum elevations well above the threshold were missed:
It is likely that the main bulk of missed passes consists of very short passes. One example is this:
Not sure what exactly is happening here, but these passes are very short and would all likely be missed by libpredict.
From the initial analysis, the current algorithms are not that bad. We want to make improvements, however, and do a clean-room implementation of the functions for our long-term goal of releasing libpredict under a LGPL-license, and do this in a more numerically correct, more numerically accurate and hopefully faster way. It will then be interesting to see how the errors compare before and after replacement, and how the time usage changes. It would also be interesting to compare against other kinds of satellite prediction software.



Leave a Reply